It is time for us to pay attention to non-deterministic polynomial time (NP-complete) problems. Non-deterministic polynomial time references non-deterministic Turing machines for problem and solutions in dealing with decisions. It is still unknown if an NP-complete problem can be solved in polynomial time on a deterministic Turing machine. What if the later statement is true? There are well known problems that can be solved in polynomial time and many others that can’t. For as long as, this Mathematical truth exists. We have built our technology in cryptosystem on the axiom that insolvability of NP problems in polynomial times gives validity to the integrity of most algorithms. This also has an implication that all along we have constructed our solutions to fit the arbitrary requirement of the computation in polynomial time.
Irreducibility of problems is not enough. This is our self-imposed limitation in computer science as not all problems fit in either polynomial time or realistic time. Such classification is the reason why the problem persists today. The question I hear all the time as desiderata of NP-Completeness is this: Given a board position in m*n generalization of a chessboard, will black guarantee a win if it moves first? My question is: Given a board position in m*n generalization of a chessboard, will the black or white knight land on all the squares (change state) -in a sweeping move without a retrace of movement to the origin position? If the answer to the later question is true.
Can this be done in polynomial time? I will say probably exponential time because the bigger the dimension the more moves you will make. Another question is. Given the knight’ legal moves: What kind of Turing machine will you call this chess board? Non-deterministic or deterministic? If it is non-deterministic, it simply means that modern encryption will have long tenure in this era as the insolvability of NP Complete problems reigns supreme. Really! Is this statement accurate? Well, we know that the polynomials used in the AES are irreducible ones. GF (2^8) field elements are created from these polynomials. Let’s re-write field equation to GF(2^P); where p=8. Will this maxim of AES hold still (quantum immune) in the wake of quantum computing, Cloud, AI and the new era –Industrie 4.0? Has anyone thought about the requirement of the Galoi Field when p > 8? These questions raise other questions while they pique our minds on the direction we must go.
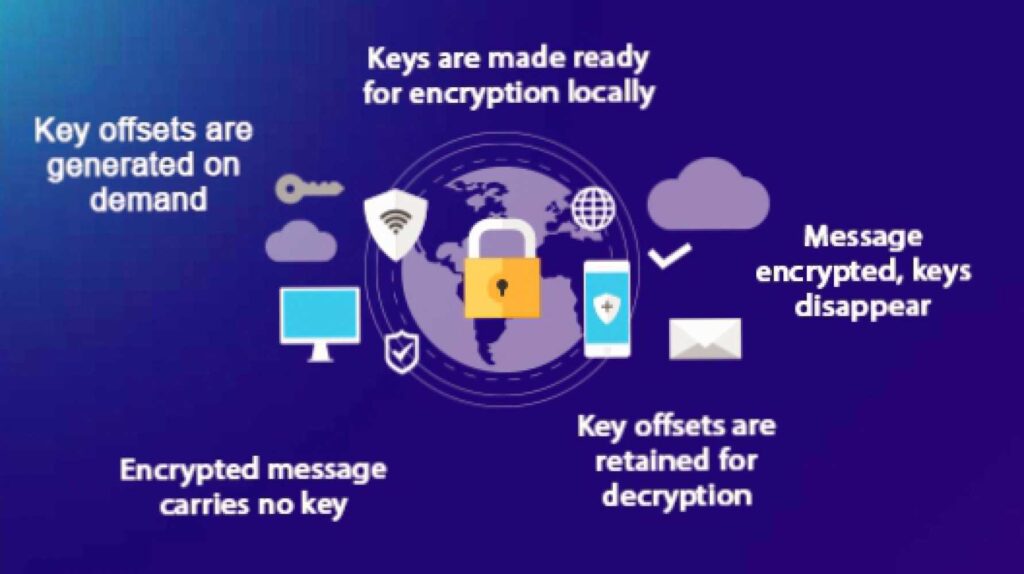
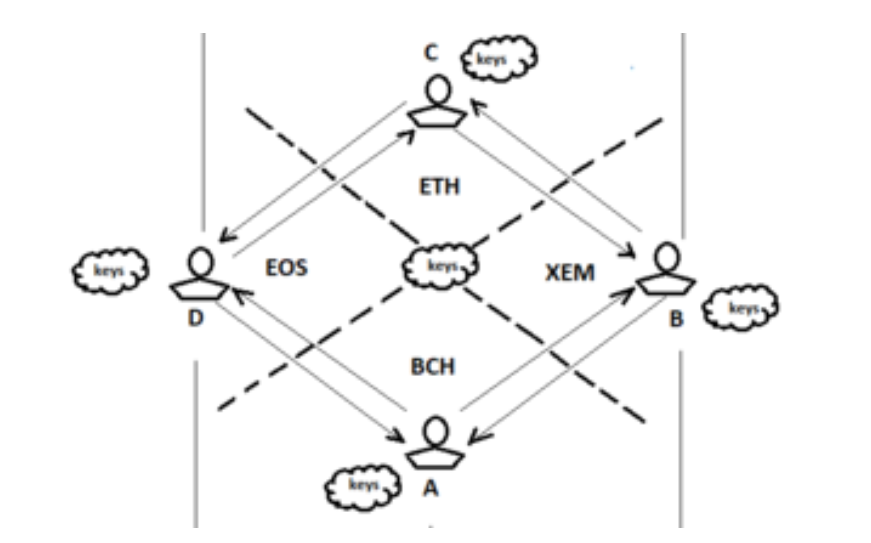
Whichever way the equation goes. There is a possibility that what is non-deterministic today could appear deterministic tomorrow especially with the rate of technological advancement. It is imperative to know that earlier on we realized that there must be an introduction of an external context into symmetric key cryptography (encryption) to keep the system firmly grounded and stabilized before the new era. This system is achieved by using numbers generated from a knight’s tour solution. LokDon have invested much time (17+ years) to develop a unique knight’s template (KT) which is a scope of 16*16 or 256 integers. It is about 680 digits long. A character set called standard state (ST) of equivalent number is mapped to the KT to build M1—A cipher template. These cipher templates we have used to encrypt messages as well as fingerprints or other grooved entities. The strings produced are encrypts which none can decipher without the knowledge of the keys used locally as well as silent password or biometric.
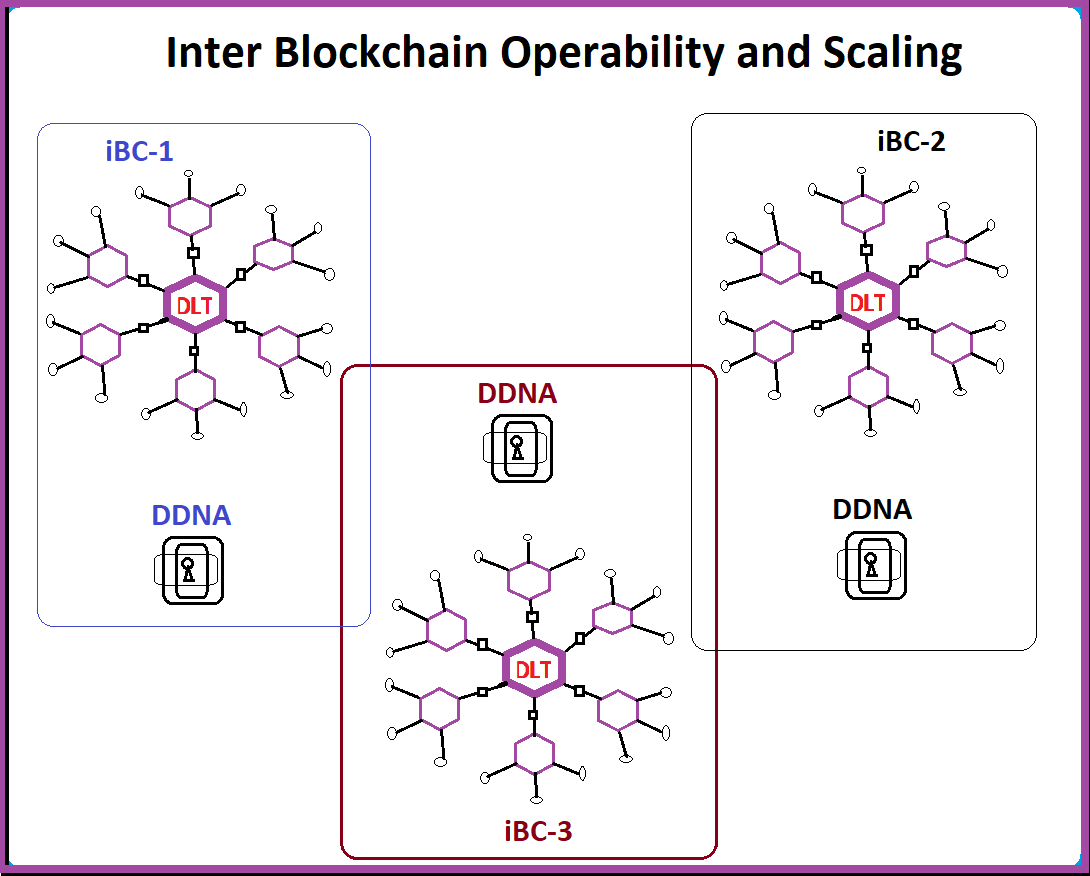
However, all these keys and templates are not saved or moved from point A to point B on any disk. They are generated on the fly. We believe that this system has all that is needed to take us to the new era of internet of things, internet of things-of-values (IoToV) and internet of values (IoV).